Inverse Transform Random Sampling - Binomial distribution from Uniform distribution.

Inverse Transform Random Sampling방법을 사용하여 Uniform distribution에서 Binomial distribution을 구하기.

• 우선, Inverse Transfor Random Sampling이 무엇인가?

개념을 간단히 정리하자면 uniform distribution으로부터 내가 알고싶은 분포를 무작위 추출(random sampling) 할 수 있도록 해주는 개념이다.

즉, uniform distribution으로부터 random sampling한 케이스들을 내가 원하는 분포의 모양으로 변환시켜줄 수 있다.

 

• inverse transform의 단계는 다음과 같다.

1.  구하고자 하는 분포의 CDF(cumulative distribution function, 누적분포함수)를 구한다.

2. CDF의 역함수를 구한다.

3. CDF의 역함수에 uniform distribution의 값들을 대입해준다.

 

(자세한 증명은 아래 링크를 참조하면 된다.)

https://youtu.be/9ixzzPQWuAY

 

• Binomial distribution(이항분포)를 Inverse Transform Random Sampling으로 구하기

우선 binomial distribution의 CDF는 이렇다고 한다...

n : 시도한 횟수, p : 사건이 일어날 확률 (출처 wikipedia)

내가 수학,통계를 잘 하는 사람들이었다면 단번에 이 함수의 역함수를 구해보려 했겠지만... 그렇지 않기 때문에 python을 통해서 문제를 해결해보려고 한다!

 

또한 uniform distribution으로부터 구한 binomial distribution이 일반적으로 표현되는 distribution과 같은 결과를 나타내는지 그래프를 통해서 시각적으로 확인해보자

import matplotlib.pyplot as plt
from scipy import stats

# binomial distribution from uniform distribution (n = 10) random sampling
uni_rvs1 = np.random.uniform(size = 10)
inv_binom_rvs = stats.binom.ppf(uni_rvs1,10,0.5)
plt.hist(inv_binom_rvs,20,width=0.5,label='inverse transform sampling')

# binomial distribution (n = 10) random sampling
binom_rvs = np.random.binomial(10,0.5,size=10)
plt.hist(binom_rvs,20,label='binomial dist')

plt.xlabel('binominal')
plt.ylabel('Frequency')
plt.title("(n = 10)")
plt.legend()

plt.show()

 

먼저 matplotlib.pyplot 과 scipy stats 모듈을 불러와주고

uni_rvs1에 n = 10일때 uniform dist의 결과값을 저장해준다.

그리고 아까 언급했었던 stats.binom.ppf라는 매서드가 우리를 대신해서 binomial 분포의 역함수 값을 구해줄 것이다.

히스토그램으로 결과를 나타내주면 아래와 같은 그림이 나타난다.

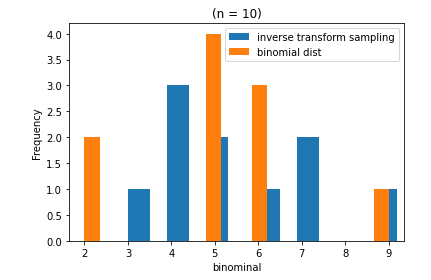
아직까지는 두 분포가 같다고 보기에는 무리가 있어보인다...

plt.subplot(1,2,1)
uni_rvs1 = np.random.uniform(size = 10)
inv_binom_rvs = stats.binom.ppf(uni_rvs1,10,0.5)
plt.hist(inv_binom_rvs,20,width=0.5)
plt.title('binom_dist Inverse transform')

plt.subplot(1,2,2)
binom_rvs = np.random.binomial(10,0.5,10)
plt.hist(binom_rvs,20)
plt.title('Binom_dist')

plt.suptitle('n=10')
plt.show()

 

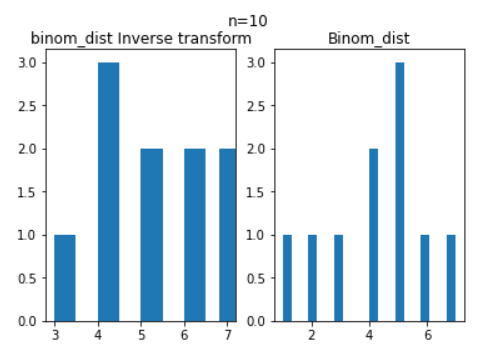
아래 그림은 같은 데이터를 subplot으로 그려본 것이다.

역시나 같은 분포라고 볼 수가 없을것 같다.

 

이제 사이즈

n = 100

n = 1000 

n = 10000

이렇게 늘려보겠다.

# binomial distribution from uniform distribution (n = 100) random sampling
uni_rvs1 = np.random.uniform(size = 100)
inv_binom_rvs = stats.binom.ppf(uni_rvs1,10,0.5)
plt.hist(inv_binom_rvs,20,width=0.5,label='inverse transform sampling')

# binomial distribution (n = 100) random sampling
binom_rvs = np.random.binomial(10,0.5,size=100)
plt.hist(binom_rvs,20,label='binomial dist')

plt.xlabel('binominal')
plt.ylabel('Frequency')
plt.title("(n = 100)")
plt.legend()

plt.show()

plt.subplot(1,2,1)
uni_rvs1 = np.random.uniform(size = 100)
inv_binom_rvs = stats.binom.ppf(uni_rvs1,10,0.5)
plt.hist(inv_binom_rvs,20,width=0.5)
plt.title('binom_dist Inverse transform')

plt.subplot(1,2,2)
binom_rvs = np.random.binomial(10,0.5,100)
plt.hist(binom_rvs,20)
plt.title('Binom_dist')

plt.suptitle('n=100')
plt.show()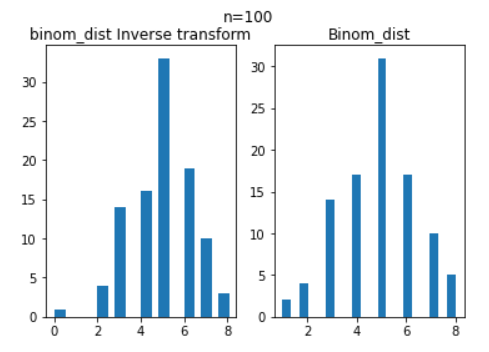

n = 100이 되니 두 분포가 점점 비슷해지는 것을 볼 수 있다.

 

 

# binomial distribution from uniform distribution (n = 1000) random sampling
uni_rvs1 = np.random.uniform(size = 1000)
inv_binom_rvs = stats.binom.ppf(uni_rvs1,10,0.5)
plt.hist(inv_binom_rvs,20,width=0.5,label='inverse transform sampling')

# binomial distribution (n = 1000) random sampling
binom_rvs = np.random.binomial(10,0.5,size=1000)
plt.hist(binom_rvs,20,label='binomial dist')

plt.xlabel('binominal')
plt.ylabel('Frequency')
plt.title("(n = 1000)")
plt.legend()

plt.show()

plt.subplot(1,2,1)
uni_rvs1 = np.random.uniform(size = 1000)
inv_binom_rvs = stats.binom.ppf(uni_rvs1,10,0.5)
plt.hist(inv_binom_rvs,20,width=0.5)
plt.title('binom_dist Inverse transform')

plt.subplot(1,2,2)
binom_rvs = np.random.binomial(10,0.5,1000)
plt.hist(binom_rvs,20)
plt.title('Binom_dist')

plt.suptitle('n=1000')
plt.show()

n = 1000 일때 이제 같은 분포라고 보아도 무방할 듯 싶다.

 

 

# binomial distribution from uniform distribution (n = 10000) random sampling
uni_rvs1 = np.random.uniform(size = 10000)
inv_binom_rvs = stats.binom.ppf(uni_rvs1,10,0.5)
plt.hist(inv_binom_rvs,20,width=0.5,label='inverse transform sampling')

# binomial distribution (n = 10000) random sampling
binom_rvs = np.random.binomial(10,0.5,size=10000)
plt.hist(binom_rvs,20,label='binomial dist')

plt.xlabel('binominal')
plt.ylabel('Frequency')
plt.title("(n = 10000)")
plt.legend()

plt.show()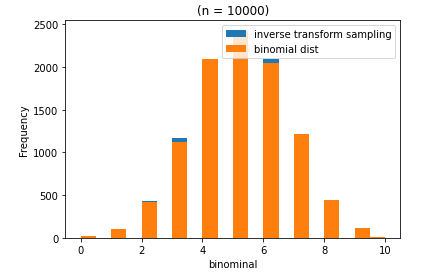

plt.subplot(1,2,1)
uni_rvs1 = np.random.uniform(size = 10000)
inv_binom_rvs = stats.binom.ppf(uni_rvs1,10,0.5)
plt.hist(inv_binom_rvs,20,width=0.5)
plt.title('binom_dist Inverse transform')

plt.subplot(1,2,2)
binom_rvs = np.random.binomial(10,0.5,10000)
plt.hist(binom_rvs,20)
plt.title('Binom_dist')

plt.suptitle('n=10000')
plt.show()

n = 10000일때 둘의 분포이다.

이제 둘의 분포가 같다고 봐도 괜찮을 것 같다.

즉 inverse transform random sampling이 잘 되고있는 것을 볼 수 있다.

 

추가로 sample의 크기가 커질수록 정규분포에 근사한다는 중심극한가설(Central limit Theorem)도 성립하는 것을 볼 수 있다.

 

읽어주셔서 감사합니다!