아이테킨의 끄적끄적

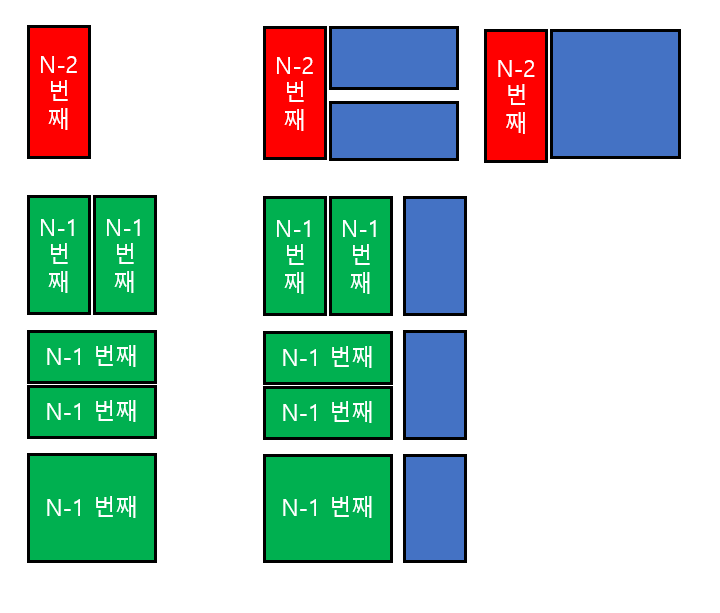
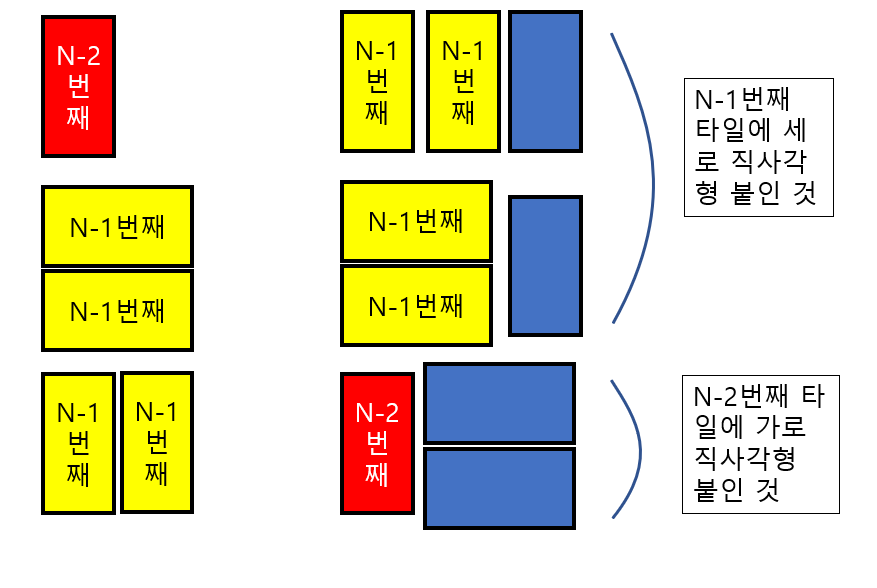
피보나치 수열을 구하는 대표적은 다이나믹 프로그래밍 문제이다. 그러나 이번 문제는 단순히 문제를 해결하는 것 뿐만 아니라 더 빨리 효율적으로 풀 수 있는 알고리즘을 물어보고 있다. 문제의 답은 반복문 또는 메모이제이션을 이용해서 풀면 된다. (메모이제이션을 이용한 코드는 아래 있다.) # 반복문으로 푼 피보나치 n = int(input()) dp = [0]*100 dp[1] = 1 for i in range(2,n+1): dp[i] = dp[i-1] + dp[i-2] print(dp[n]) 이번 기회에 피보나치 수열을 구하는데 사용되는 3가지 방법에 대해서 정리해보았다. 반복문, 재귀, 메모이제이션 총 세가지 방법으로 피보나치 수열을 풀 수 있지만 각각 시간복잡도, 메모리를 사용하는 정도가 다르다. 1...

다이나믹 프로그래밍 문제는 점화식을 풀어서 해결해야 하는 경우가 많다는 것을 기억하자. 이 문제도 점화식을 사용해보면 해결할 수 있다. i번째 포도주를 시음한다고 하면 생각할 수 있는 경우의 수는 1. i-2번째 포도주를 마신 경우 2. i-3번째 i-1번째 포도주를 마신 경우 또한 i번째 포도주를 마시지 았았을 경우 생각할 수 있는 경우의 수는 3. i-1번째 포도주를 마신 경우이다. 이 세가지 경우의 수 에서 가장 큰 값을 출력해내면 된다. 이를 점화식으로 표현해보면 dp[i] = max(dp[i-2]+w[i], dp[i-3]+w[i-1]+w[i], dp[i-1]) # 2156번: 포도주 시식 # dp문제는 점화식을 만들어봐야 한다. # 다시 풀어보기!! 아 실력이 안느냐 왜 ㅠㅠ n = int(in..

# 1912번: 연속합 n = int(input()) a = list(map(int, input().split())) sum = [a[0]] for i in range(len(a) - 1): sum.append(max(sum[i] + a[i + 1], a[i + 1])) print(max(sum))

DP문제로 이 문제는 뒤에서부터 생각해야 풀 수 있다. 뒤에서 풀어보려고 계속 노력하다가 결국엔 다른 사람의 블로그를 참고해서 풀었다. 참고 블로그 https://pacific-ocean.tistory.com/199 # 14501번: 퇴사 n = int(input()) t_list = [] p_list = [] for _ in range(n): t,p = map(int,input().split()) t_list.append(t) p_list.append(p) dp = [0]*(n+1) for i in range(n-1,-1,-1): if t_list[i] + i > n: dp[i] = dp[i+1] else: dp[i] = max(dp[i+1],p_list[i] + dp[i + t_list[i]]) pr..

DP문제다 DP문제의 가장 큰 특징은 중복되는 서브문제(overlapping subproblem)와 최적 부분 구조(optimal substructure)로 이런 유형의 문제에 접근하기 위해서는 하나의 문제를 작은 그러나 같은 방법으로 풀 수 있는 문제로 쪼개야한다. 이번 문제에서는 원하는 카드의 개수를 만드는 최대값을 구해야한다. 카드 1개 샀을때 최대값 카드 2개 샀을때 최대값 카드 3개 샀을때 최대값 카드 4개 샀을때 최대값 이런식으로 생각을 해보면 카드 1개 -> P[1] (=1개 카드 값) 카드 2개 -> max(P[1]+P[1] , P[2]) 카드 3개 -> max(P[1]+P[1]+P[1] , P[1]+P[2] , P[3]) ... 이런식으로 모두 따져봐야 하는 문제다. #11052번: 카드..

앞서 풀었던 타일 문제에 정사각형 타일이 하나 추가된 문제이다. 정사각형 모양의 타일이 하나 추가되었기 때문에 n-2번째 타일에서 가로 직사각형 두개 붙이는 경우와 정사각형 붙이는 경우, 총 두가지 방법으로 늘어났다. m(n) = m(n-1) + (2 × m(n-2)) # 11726번: 2xn 타일링 n = int(input()) m = [0]*1001 m[1] = 1 m[2] = 2 for i in range(3,n+1): m[i] = m[i-1] + m[i-2] print(m[n]%10007)

LIS(Longest Increasing Subsequence)라는 유명한 DP 문제라고 한다. 처음봤다. 아이디어는 배열에 있는 숫자들을 각각 비교하면서 큰 숫자가 나올때마다 1을 더해주는 방법이다. 배열의 순서에 상관없이 증가하는 가장 긴 부분수열의 길이를 찾을 수 있다. (배열의 최대값이 답이다) # 11053번: 가장 긴 증가하는 부분 수열 # LIS(Longest Increasing Subsequence)라는 유명한 DP문제 N = int(input()) A = list(map(int,input().split())) dp = [1] * N for i in range(N): for j in range(i): if A[j] < A [i]: dp[i] = max(d[i],dp[j]+1) print(m..

예전에 공부할때 봤었던 이코테라는 책에 이 문제와 비슷한 유형이 있어서 쉽게 풀 수 있었다. 타일을 채우는 방법의 수를 구하는 문제인데 m(n) = m(n-1) + m(n-2)로 결국 피보나치 수열과 같다. 피보나치 수열은 DP의 대표적인 문제로 재귀와 반복문 둘다 풀이가 가능하고 둘다 알아놓으면 좋을 듯 하다. 이번에는 바텀업 방식으로 풀어보았다. 마지막에 10007로 나눈 나머지를 출력하는 것을 까먹으면 안된다 ㅠㅠ 이걸 놓쳐서 10분동안 "어.. 왜 안되지...??" 를 반복했다.ㅠㅠ # 11726번: 2xn 타일링 n = int(input()) m = [0]*1001 m[0] = 0 m[1] = 1 m[2] = 2 for i in range(3,n+1): m[i] = m[i-1] + m[i-2] ..

일반적인 DP문제다. 오랜만에 문제를 풀어서 그런지(코딩 자체가 굉장히 오랜만이다...ㅠㅠ) 문제를 해결하는데 생각보다 오랜 시간이 들었던거 같다. 다이나믹 프로그래밍 문제는 기본적으로 문제를 작게 잘 쪼개는것이 가장 중요하다고 생각한다. 재귀를 이용해서 풀던(탑다운), 반복문을 이용해서 풀던(바텀업) 자기가 생각하기 편한 방식대로 풀면 된다. [DP조건] 중복되는 서브문제(overlapping subproblems) - 문제해결관점 : 큰 문제를 작은 문제로 쪼갤 수 있고, 큰문제와 작은문제를 같은 방법으로 풀 수 있다. => 메모이제이션 최적 부분 구조(optimal substructure) - 문제의 구조관점 : 전체 문제의 최적해가 부분 문제의 최적해들로써 구성된다. 이 문제는 주어진 수의 3번째..

점화식 $$ a_n = min(a_{n/3}+1, a_{n/2}+1, a_{n-1}+1) $$ 코드 # 1463 - 1로 만들기 n = int(input()) dp = [0] * (n+1) for i in range(2,n+1): dp[i] = dp[i-1]+1 if i%3 == 0: dp[i] = min(dp[i//3]+1, dp[i]) if i%2 == 0: dp[i] = min(dp[i//2]+1, dp[i]) print(dp[n])