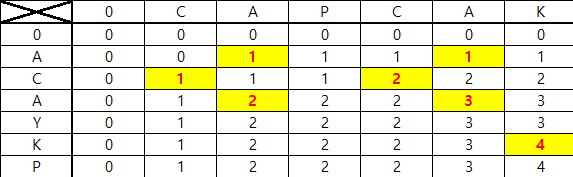
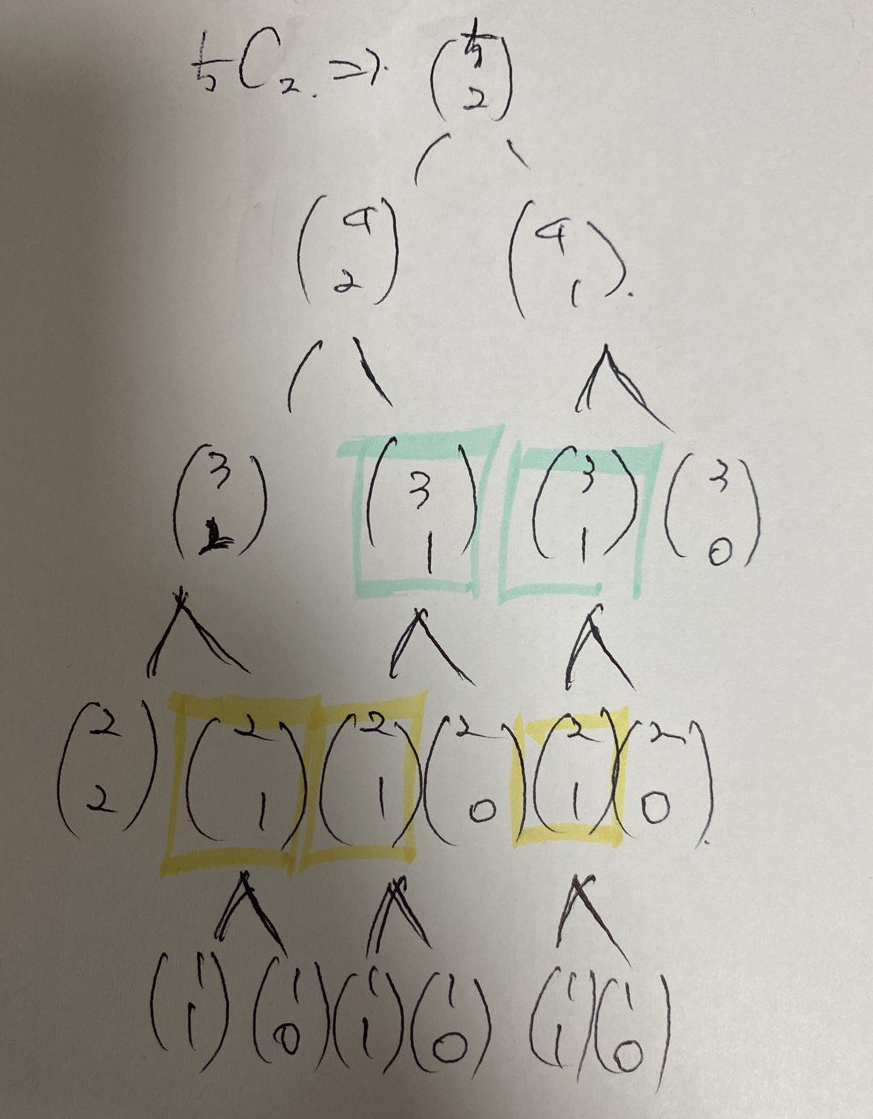이항계수를 구하는 구하는 알고리즘을 짜면 되는 문제이다. 1. 이항계수의 정의를 이용하여 그대로 구현! 이항계수를 구하는 공식은 고등학교때 당연히 배웠지만 까먹었다 해도 문제는 없다. 우리에겐 구글이 있기 때문에...!! 구글에 이항계수만 검색해도 친절하게 설명해주는 블로그와 사이트들이 많이 있다. 자신이 보기 편한 것을 보고 이해하고 그 공식을 구현하면 쉽게 풀리는 문제이다. 사실 이미 알고있는 공식을 구현하기만 되는 것이라 따로 머리를 크게 쓰고 아이디어를 짜낼 필요도 없다. 아래의 첫번째 코드가 이항계수의 공식을 가장 충실히 따라 알고리즘을 구현한 코드이다. python에는 math라이브러리에 펙토리얼을 구할 수 있는 기능들이 있지만 연습도 할 겸, 코드량도 많지 않으니 팩토리얼 함수를 구현하여 이..